Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
Tags
- ML
- 상향식 힙
- 선형조사법
- 연결리스트
- nodejs
- anaconda
- pytorch
- 경사하강법
- vsCode
- 힙정렬
- upheap
- 이중해싱
- 해시테이블
- bodyparser
- 이중연결리스트
- 알고리즘
- MSE
- urlencoded
- 분리연쇄법
- 선형회귀
- downheap
- Loss함수
- 2차조사법
- POST
- body-parser
- 삽입식 힙
- 딥러닝
- 개방주소법
Archives
- Today
- Total
LittleDeveloper
Week12_위상정렬_실습 본문
방향그래프?
1. 방향 비사이클 그래프(DAG)
2. 방향 사이클 => 위상순서 x
위상정렬?
위상 정렬(topological sort): DAG로부터 위상순서를 얻는 절차
방향그래프의 위상순서(topological order) : 모든 i < j인 간선 (vi , vj )에 대해 정점들을 번호로 나열한 것
위상정렬 알고리즘
1. DFS
=>더이상 나가는 간선이 없는 정점부터 번호 매김
2. 각 정점의 진입차수 이용
=>들어오는 간선이 없는 정점부터 번호 매김
-아래의 위상 정렬 알고리즘은, 두 번째 알고리즘이며,
1)인접정점리스트에서 새로 입력되는 간선에 대한 노드가 리스트의 '맨 앞에' 삽입됨 (*단순연결리스트 addFirst() )
2)최초로 진입간선의 개수가 0인 정점을 찾을 때, '정점 번호 순서대로' 조사됨.
**필요한 자료구조**
=>큐!
:정점들의 대기열
<큐 템플릿>
//큐 구조체 정의-원형큐
typedef struct{
char elem[SIZE];
int front, rear;
}QueueType;
//큐 초기화
void initQueue(QueueType* Q)
{
Q->front = Q->rear = 0;
}
int isEmpty(QueueType* Q) {
return Q->rear == Q->front;
}
int isFull(QueueType* Q) {
return (Q->rear + 1) % SIZE == Q->front;
}
//삽입
void enqueue(QueueType* Q, char vName) {
if (isFull(Q)) {
printf("FULL\n");
return;
}
Q->rear = (Q->rear + 1) % SIZE;
Q->elem[Q->rear] = vName;
}
//삭제
char dequeue(QueueType* Q) {
if (isEmpty(Q))
{
printf("EMPTY\n");
return 0;
}
Q->front = (Q->front + 1) % SIZE;
return Q->elem[Q->front];
}
<--그래프 템플릿-->
//간선 구조체 없어도 됨
//인접정점
typedef struct IncidentEdge{
char aName;
struct IncidentEdge* next;
}IncidentEdge;
//정점
typedef struct Vertex{
char vName;
IncidentEge* iHead;
struct Vertex* next;
}Vertex;
//그래프
typedef struct{
Vertex* vHead;
int vCount;
}Graph;
void init(Graph *G){
G->vHead=NULL;
G->vCount=0;
}
void makeVertex(Graph *G, char vName){
Vertex* v=(Vertex*)malloc(sizeof(Vertex));
v->vName=vName, v->next=NULL;
v->iHead=NULL, G->vCount++;
Vertex* q=G->vHead;
if(q==NULL){
G->vHead=v;
}
else{
while(q->next!=NULL){
q=q->next;
}
q->next=v;
}
}void makeIncidentEdge(Vertex* v, char aName){
IncidentEdge* p=(IncidentEdge)*malloc(sizeof(IncidentEdge));
p->aName=aName, p->next=NULL;
IncidentEdge*q=v->iHead;
if(q==NULL) v->iHead=p;
else{//부착리스트의 맨 앞에 삽입
p->next=q;
v->iHead=p;
}
}
Vertex* findVertex(Graph *G, char vName){
Vertex* p=G->vHead;
while(p->vName!=vName)
p=p->next;
return p;
}
void insertEdge(Graph *G, char v1, char v2){
Vertex* v=findVertex(G,v1);
makeIncidentEdge(v,v2);// 정점 v1과 v2 연결해주기
}
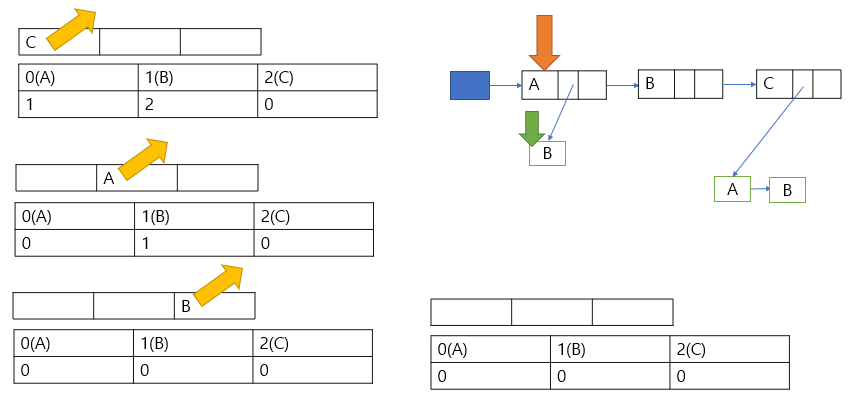
*입력 예시 2는 방향 사이클, 즉 순환하므로 위상 순서가 존재하지 않는다.
//a의 아스키 코드: 97, A: 65
void inDegree(Graph* G, int in[]) {
Vertex* p = G->vHead;
IncidentEdge* q;
char ch;
for (; p != NULL; p = p->next) {
for (q = p->iHead; q != NULL; q = q->next) {
ch = q->aName;
//if (ch >= 'A' && ch <= 'Z')code = 65;
//else if (ch >= 'a' && ch <= 'z')code = 97;
//else if (ch >= '0' && ch <= '9') code = 48;
in[q->aName - 65]++; //내차수 증가
}
}
}
int topologicalSort(Graph* G, int in[]) {
QueueType Q;
initQueue(&Q);
Vertex* p;
IncidentEdge* q;
int flag = 0;
inDegree(G, in);
//내차수 0이면 큐에 삽입
for (int i = 0; i < G->vCount; i++) {
if (in[i] == 0) {
flag = 1;
enqueue(&Q, i + 65);
}
}
//내차수 0인 요소가 없음 => 사이클
if (flag == 0) return 0;
//for (int i = 0; i < G->vCount; i++) printf("%d ", in[i]);
//printf("\n");
while (!isEmpty(&Q)) {
char vName = dequeue(&Q);
printf("%c ", vName);
p = findVertex(G, vName);
q = p->iHead;
while (q != NULL) {
in[q->aName - 65]--; //내차수 감소
if (in[q->aName -65] == 0) {
enqueue(&Q, q->aName);
}
q = q->next;
}
//for (int i = 0; i < G->vCount; i++) printf("%d ", in[i]);
//printf("\n");
}
return 1;
}'알고리즘(C)' 카테고리의 다른 글
| Week11_그래프순회_BFS_실습 (0) | 2021.12.03 |
|---|---|
| Week11_그래프순회_DFS_실습 (0) | 2021.12.02 |
| Week10_그래프_실습 (0) | 2021.12.01 |
| Week9_해시테이블_실습(2) (0) | 2021.11.29 |
| Week9_해시테이블_실습(1) (0) | 2021.11.29 |




