| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- 선형조사법
- 개방주소법
- 힙정렬
- 2차조사법
- 경사하강법
- ML
- 이중연결리스트
- body-parser
- 이중해싱
- vsCode
- MSE
- urlencoded
- bodyparser
- pytorch
- Loss함수
- anaconda
- 딥러닝
- 상향식 힙
- downheap
- 해시테이블
- POST
- nodejs
- 알고리즘
- 분리연쇄법
- 선형회귀
- 연결리스트
- 삽입식 힙
- upheap
- Today
- Total
LittleDeveloper
모두의 딥러닝 4장 경사하강법 본문
우리는 지난 시간에 선형회귀법에서 기울기 a의 크기가 너무 크거나 너무 작으면, 오차(실제값과 예측값의 차)가 커짐을 확인했다. 저번에 다루지 않았던 개념이 하나 있는데, 'Loss 함수'가 무엇인지부터 짚고 넘어가보자.
Loss 함수란?
= 실제 값과 예측 값 차이(오차)의 제곱의 합
오차가 작을수록 좋으니까, Loss 함수가 작을수록 좋은 모델이 된다는 것을 알 수 있다.
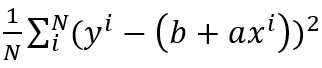
위의 공식에서 a(기울기), b(y절편) 값에 따라 Loss 함수를 조절할 수 있다. Loss 함수를 최소화하는 a, b 값을 찾기 위해 도입된 방법에는 여러가지가 있다.
1) Gradient descent (경사하강법)
2) Normal equation (least squares)
3) Brute force search
4) etc..
이번 시간에는 첫번째 방법을 자세히 알아보자!
경사하강법이란?
Loss함수 값이 최소가 되는 절편, 기울기를 각각 b', a' 이라고 하자.
경사하강법은 계산 한번으로 b', a'를 구하는 것이 아니라, 초기값에서 점진적으로 구하는 방식이다.
그 점진적인 과정을 자세히 살펴보면,
1) b, a 값을 랜덤하게 초기화한다.
2) 현재 b, a 값으로 Loss 값(오차)을 계산한다.
3) 현재 b, a 값을 어떻게 바꿔야 Loss 값을 줄일 수 있는지 알 수 있는 'Gradient 값'을 계산한다.
4) 이 Gradient 값을 활용하여 b, a 값을 갱신한다.
5) Loss 값이 최소화될 때까지 2)~4)을 반복한다.
Loss 값까진 알겠는데 Gradient 값은 또 뭐야..? 라고 생각할 수 있다.
Gradient값은 그냥 별거 없고 '기울기값'을 뜻한다. 무엇의 기울기를 말하냐면...
우리가 Loss함수를 그려보면 대략적으로 아래처럼 이차함수같이 생겼다.
그리고 이 이차함수의 각 점마다 미분계수, 즉 기울기(Gradient)가 있을 것인데.. '기울기의 절대값'이 최소가 되는 지점은 어디가 될까??
-> 초기값으로 a=4, b=-4인 접선을 하나 그어보자.
y=4x-4
접점 (2,4)에서는 기울기가 최소가 되지 않는다. 그러면 다음번에는 기울기가 +가 아닌 -가 되는 접점으로 이동해보자. (==>바로 여기서 얼마만큼 이동할지 고민하게 되는데, 이 이동거리를 우리는 '학습률(Learning rate)'라고 부르기로 정했다.)
이런 식으로 기울기의 절대값을 줄여나가다 보면, 이 값이 0이 되는 지점이 나온다.
그렇다, 바로 이차함수의 최솟값이다. ( 아래 그래프에서는 (0,0) ) 이 지점에서 순간기울기가 0이 된다.

이제 Colab에서 코드로 경사하강법을 구현해보자.
먼저 필요한 pip를 불러오고...
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt지난 시간에 썼던 (X:평균 기온- Y:판매량) 데이터를 그대로 써보자.
x=[2,3, 4.5, 6, 7.8, 9.6, 12, 12.4, 13, 15, 15.2, 16.8, 19.4, 20, 21, 23.2, 24] #평균 기온
y=[8, 18,24,20,30,40,46,50,55,59,64,56,69,59,70,67,78] #판매량#그래프로 나타내기
plt.figure(figsize=(8,5))
plt.scatter(x,y)
plt.show()
#리스트로 된 X,Y값을 numpy배열로 바꾸기
x_data=np.array(x)
y_data=np.array(y)#기울기 a와 y절편 b의 값 초기화
a=0
b=0#학습률 정하기
learning_rate = 0.003#몇 번 반복될지 설정
epochs = 2001#경사하강법
for i in range(epochs):
y_pred = a*x_data + b #예측값
error = y_data - y_pred #오차
#오차 함수를 a로 미분한 값
a_diff = -(2/len(x_data))*sum(x_data*error)
#오차 함수를 b로 미분한 값
b_diff = -(2/len(x_data))*sum(error)
#학습률을 곱해 기존의 a,b 값 업데이트
a = a - learning_rate * a_diff
b = b - learning_rate * b_diff
if i%100==0:
print("epoch=%.f, 기울기=%.04f, 절편=%.04f" %(i,a,b))
#앞서 구한 기울기와 절편 이용해 그래프 다시 그리기
y_pred = a*x_data+b
plt.scatter(x,y)
plt.plot([min(x_data),max(x_data)],[min(y_pred),max(y_pred)])
plt.show()경사하강법으로 구한 a, b 값으로 그린 아래와 같은 직선 그래프를 확인할 수 있다!!
2000번째 예측에서는 a=2.8894, b=9.5854 가 나왔다.
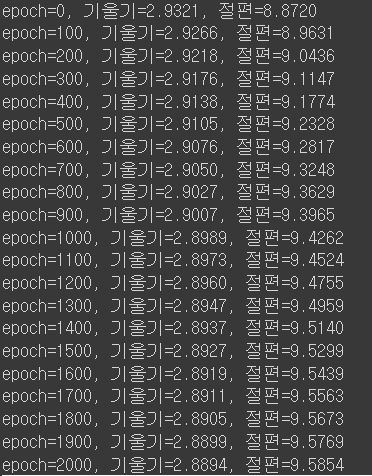

지난 시간에 최소제곱법으로 구한 결과가 아래와 같은 것을 떠올려보면 거의 똑같은 결과가 나왔음을 확인할 수 있다!

그런데.... 사실 오류가 발생했었다...
처음에 학습률을 0.3으로 설정했는데, 초기값만 멀쩡하고 그이후로 기울기와 절편값이 nan가 나와서 당황스러웠다,,
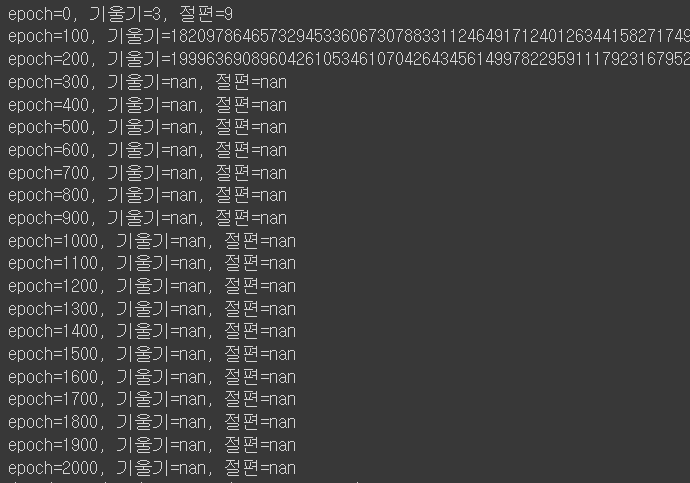
그래서 서치해본 결과 비슷한 이슈를 가진 사례들이 있었고, learning rate가 너무 큰 것이 원인이어서 이를 좀더 작게 조절해서 (0.03 -> 0.003) 올바른 결과를 도출할 수 있었다!
다시 돌아와서! 다음 개념으로 넘어가보자. 지난 시간에 '단순 선형 회귀'만 다루었는데, 이번에는 '다중 선형 회귀'를 알아보자.
다중 선형 회귀란?
지금까지는 아이스크림 판매량(Y)에 영향을 끼치는 입력값이 평균기온(X) 하나였는데, 우리의 실제 삶에서는 사실 Y에 영향을 주는 요소가 훨씬 더 많을 것이다. 즉, 입력값 X가 많은 경우가 생긴다면, 이에 대한 정확한 예측 방법이 필요할 것이다.
따라서 지금부터는 평균기온을 x1, 평균강수량을 x2 라고 해보자. 그러면 아래와 같은 관계식을 얻을 수 있다.
y = a1*x1 + a2*x2 + b
이때 a1, a2는 또 어떻게 구할까? ==> 앞서 배운 '경사하강법'을 쓰자!!
이 경우에는 각 개별 x¡ 에 해당하는 최적인 a¡ 를 찾아야 한다. 다중 선형 회귀 모델에서 Y와 X의 관계식을 표현하면...
Y ≒ a¡x¡ + ...+a3*x3+ a2*x2+ a1*x1 + b
인데, 우리의 경우에는 입력값이 2개니까 Y ≒ a1 *x1 + a2*x2 + b 로 나타낼 수 있다.
또한 단순 선형 회귀와 마찬가지로 Loss 함수는 (입력값과 실제값)^2 로 정의하며, 역시 b, a1, a2, a3... a¡ 을 조절하여 Loss 함수의 크기를 작게 해야 한다.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
#입력값 x2 추가
x1=[2,3, 4.5, 6, 7.8, 9.6, 12, 12.4, 13, 15, 15.2, 16.8, 19.4, 20, 21, 23.2, 24] #평균 기온
x2=[13.4, 11, 9, 10.5, 8.9, 8,4.3, 4, 4.7, 5, 2.1, 4, 1.7, 4.7, 0.43, 0.5, 0] #평균 강수량
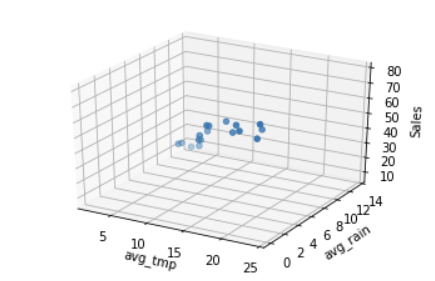
y=[8, 18,24,20,30,40,46,50,55,59,64,56,69,59,70,67,78] #판매량#그래프 확인
ax = plt.axes(projection='3d')
ax.set_xlabel('avg_tmp')
ax.set_ylabel('avg_rain')
ax.set_zlabel('Sales')
ax.dist =11
ax.scatter(x1,x2,y)
plt.show()
x1_data = np.array(x1)
x2_data = np.array(x2)
y_data = np.array(y)a1 = 0
a2 = 0
b = 0learning_rate=0.003epochs=2001#경사하강법
for i in range(epochs):
y_pred = a1*x1_data + a2*x2_data + b #예측값
error = y_data - y_pred #오차
#오차 함수를 a1로 미분한 값
a1_diff = -(2/len(x1_data))*sum(x1_data*error)
#오차 함수를 a2로 미분한 값
a2_diff = -(2/len(x2_data))*sum(x2_data*error)
#오차 함수를 b로 미분한 값
b_diff = -(2/len(x1_data))*sum(y_data-y_pred)
#학습률을 곱해 기존의 a1, a2, b 값 업데이트
a1 = a1 - learning_rate * a1_diff
a2 = a2 - learning_rate * a2_diff
b = b - learning_rate * b_diff
if i%100==0:
print("epoch=%.f, 기울기1=%.04f, 기울기2=%.04f 절편=%.04f" %(i,a1,a2,b))

이렇게 다중 선형 회귀 문제에서 기울기 a1, a2, b 값까지 찾아 확인했다!
다음 시간에는 '로지스틱 회귀'를 주제로 학습해보자. 굳굳!
'AI' 카테고리의 다른 글
| Pytorch로 시작하는 딥러닝 입문- 6. 인공신경망 (0) | 2022.03.09 |
|---|---|
| AI 실무교육 2주차 (1) Neural Network 기초 (feat. Pytorch) (0) | 2022.01.16 |
| 모두의 딥러닝 3장 선형회귀법 (1) | 2022.01.08 |
| AI 실무교육 1주차 (2) 가상환경 세팅(feat. Anaconda) (0) | 2022.01.08 |
| AI 실무교육 1주차 (1) OT & 가상환경 세팅 (3) | 2022.01.07 |




